Important Foreword (February 2001)
This article was proposed in May 2000 for publication in an eminent European Acoustics Review. It was rejected, judged too profuse, too speculative, by both reviewers.
I submitted it to a prominent French researcher in the same psychoacoustic field, who gave a similar judgment. These reviews are reproduced below in Appendix IV.
Finally, instead of persisting in review publishing, which would mean several months of additional work and rewriting, including substantial cuts, I decided to make the present internet edition of the work, substantially unchanged, with the hope that somebody in the world would find interest in it and draw some benefit. If you occasionnal reader, appreciate this work, please make it known to other scientists and researchers in the same or near fields.
Apart a few formal adaptations for the web presentation, the only significant changes to the original submission are:
- use of color in figures, with same legibility in black and white printing
- separate edition of the figures with legends, for economical color printing (Appendix I).
- addition in Appendix II of data tables supplementing interval results figures, i.e. Figures 3-6, 9-11, 13 and 14.
- addition of figures and legends summarizing an important result too briefly cited in text (end of paragraph 5.4) about PBa Sixths experiments (Appendix III).
- publication of the reviewing appreciations, with author's final comments (Appendix IV).
SUMMARY
Abstract
![]()
1. Introduction
![]()
2. Experimental means and methods
(this section can be skipped, except §§ 2.2 Stimuli, and 2.3 Subjects).
![]()
3. Two timbres unison experiments
![]()
4. Discussion I
![]()
5. Interval experiments
![]()
6. Discussion II
![]()
7. Summary and final remarks
![]()
Acknowledgments
![]()
References
(end of original submission)
Appendix I
Appendix II
Appendix III
Appendix IV
Melodic interval performance rely on natural brain structures
Pierre Billaud
Private researcher (pierre.billaud0498@orange.fr)
Abstract
Experimental studies of melodic unison and intervals in various conditions lead to a hearing concept and a melodic interval process model, where the role of auditory images is emphasized. These models are discussed and compared to existing theories. The innate or natural origin of consonant intervals and of basic musical scales is asserted.1. Introduction
Referring implicitly to the persistent and obvious distaste of average music lovers for contemporary "music", Pierre Boulez said one day that these were "intoxicated by Schubert and Mozart". He thus denied any direct physiological basis for tonal music, which would presumably be favored only by accustoming or teaching.Since tonal music is based mainly on some "natural intervals", in melody (successive tones), as well as in harmony (simultaneous tones), it appeared desirable to identify and examine the physiological features backing the obvious existence of these natural intervals.
The present study concerns essentially melodic intervals which, contrary to harmonic, do not include immediate physical frequency relations. Its primary aim was to obtain evidence of existence in brain of permanent structural features directly enabling simple frequency ratios such as 5/4, 3/2, 2, and others, which are supposed to correspond to the well known intervals of diatonic scale and tonal music. Further, these features were expected to appear innate or developing in early years from auditory experiences more common than elaborate music listening or teaching.
Until now little research has been devoted explicitly to melodic musical intervals, with the exception of a few pure tone octave measurements (Ref.1,2). The basic idea of the present work was to perform melodic intervals with colored tones, the spectra of which would contain mainly low order strong partials, and see what occurred in terms of justness and precision, as function of harmonic content. Pure tones would be occasionally used, for comparison. For that, a Special Tone Generator and Pitch Recorder (STGPR) was devised and built, covering the low and medium auditory range.
At the very beginning of STGPR use, a strange fact happened with author as subject. When listening to a colored tone, a sudden change of timbre caused a jump of heard pitch, quite significant. This subjective timbre shift depended on spectra, frequency, and hearing side. A more thorough study of this phenomenon, very probably correlated to author's hearing impairment, led quite logically to the proposal of a hearing concept, called "subharmonic retransmission model", similar in some respects to Terhardt's (Ref.3).
A number of interval experiments were performed, with author and four normal listeners as subjects, showing clear influence of timbre.
These results are further discussed in the frame of a melodic interval process model, expanding the previously proposed hearing concept, and confirming a mental matching operation for melodic interval performance.
Some prominent other experiments and theories are considered in the light of the present proposals (Ref.4,7,10-12).
Finally the existence of physiological features of natural origin supporting melodic intervals can be safely asserted.
2. Experimental means and methods
2.1. Apparatus
All the experiments have been performed with an original device, the SPECIAL TONE GENERATOR AND PITCH RECORDER (STGPR). The STGPR includes a master permanent quartz oscillator at 64 MHz, very accurate and constant, a programmable divider D fed by a dividing number d, a tone synthesis section, a memory M of 2048 words of 14 bits, displays, and control means. The fundamental sound frequency obtained is 1 MHz/d. The maximum d being 16324, the lowest fundamental pitch lies near 60 Hz. The highest useful fundamental frequency depends on the desired precision in pitch. If one wants a precision of one savart (i.e. 4 cents, rather ambitious for melody), the upward limit will be about 2300 Hz, which leaves a rather comfortable range to investigate. The displays concern the dividing number d expressed in octal system, and the address parameters in two groups of two decimal digits each, the melodic key number (0 to 31), and the round number (0 to 63). The control means fall into four separate groups. A melodic keyboard KM of 16 keys, doubled to 32 by a common auxiliary bar, a group of 3 keys controlling the choice of melodic keyboard round RND among 64 possibilities, a capture-read/write-tuning control CRWT of four large keys, and a timbre-switching command TC of 10 keys. All keys are fixed metallic pads with epidermic sensitiveness, feeding appropriate switching circuits. Sounds are heard through intrinsic preamplifiers, external conventional stereo amplifier, and headphones BST SH10.
The KM keyboard is by design strictly melodic, i.e. with only one key active at a time. In normal interval experiments the right hand deals with the CRWT four keys, and the left with KM, RND and TC, but sometimes the right hand is used to actuate the reference key, the pitch of which must remain constant, in order to avoid any reference loss by inadvertent action on CRWT.
When a key of KM is touched, RND being fixed and a timbre chosen, an address is reached in M, and a tone is produced, the fundamental of which results of the divider d stored in this address. The divider d is the 14 bits output of an auxiliary up-down binary counter under the control of CRWT. Actuating CRWT causes finally the pitch to vary at convenience, then at release leaves the last divider value inscribed in the address played.
This device has proved fully efficient, and of relatively easy handling after a while of accustoming. Further details on this machine are given in (Ref.13).
2.2. Stimuli
The STGPR produces 10 different synthetic tones, of which only the following few are concerned here :
- Sinonde, a sine wave pure tone, at fundamental
- Flutes F1, F2, F4, soft tones of organ gedekt quality, at fundamental, octave, and double octave, respectively
- Sesquialtera, a soft tone with strong ranks n°3 and 5 and only odd harmonics
- Trompe, similar to organ reed Trumpet (full spectrum)
- Cromorn, similar to organ reed Cromorne (only odd harmonics)
The Sesquialtera is so called after a classical organ mixture stop of two ranks, a 2 2/3 foot and a 1 3/5 foot, used to colour 8 foot combinations by introducing n°3 and 5 harmonics. Its tone quality recalls clarinet in low register.
An "even" imitation of Sesquialtera, called "Octave Choir" is obtained by adding the two octave flutes F2 and F4, to the Sinonde weakened to a minimum (-18 dB) by the balance control of the stereo amplifier, taking advantage of the separate preamplifier outputs. The final mixing is effected by the headphone controls, enabling either binaural or monaural use. Adjunct of a minimum fundamental component is indispensable to avoid natural octaviation of the F2 and F4 alone. This mixture, similar to some organ ensembles (foundation stops), is felt as a rather "round" unique tone, quite different from Sesquialtera. It presents strong harmonics n°2 and 4, a weak fundamental at -18 dB, and rapidly negligible upper ranks, the strongest being n°6 and 12, at -19 dB.
The voltage functions of some of these tones are given in Figure 1. The output peak-to-peak voltages are comparable, and their hearing loudness is adjusted with the amplifier volume control, and ultimately at headphone. Figure 2 gives relative computed spectra up to the 24th rank of the used tones or mixtures : Octave Choir, Sesquialtera, Cromorn, Trompe.
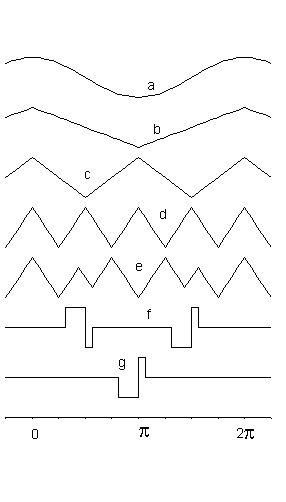 Figure 1. Forms of the voltage functions of some primary tones. From top to bottom: Sinonde(a), F1(b), F2(c), F4(d), Sesquialtera(e), Cromorn(f), Trompe(g). The respective phases shown are the real ones. |
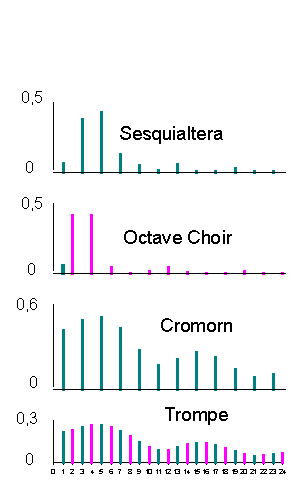 Figure 2. Relative spectra of complex stimuli (first 24 orders only). Colours: Green for odd partials, Pink for even partials. |
The onset and shut off of tones result of plain electronic switching, without progressivity (assumed irrelevant for interval experiments).
The hearing loudness was adjusted for each listener and session at a fixed "best level of hearing comfort" over the entire frequency range of the particular session.
2.3. Subjects
- PB (author) is an aged man, well acquainted with musical acoustic matters, currently practising gregorian chant. His hearing is deeply impaired, as probably the result of abnormal hearing experiences suffered during World War II. A recent audiogram of this subject indicates for right ear losses of 44 dB at 500 Hz, 70 dB at 2000 Hz, 76 dB at 4000, and 65 dB at 8000 Hz. Left ear is even worse, with up to 100 dB at 2000 and 4000 Hz. Of course these measurements are sensitivity thresholds, and when the sources intensity is sufficient, subject recovers some high frequency perception. In Experiment Ia, PB used bare left ear (designation : PB-LE). Now PB uses for right ear a hearing prothesis which compensates for losses up to 4500 Hz, with an auto-adjusting volume range of some 15 dB. This device is present in monaural experiments Ib and further (aided subject designation : PBa).
- Lady CR is a vocal artist, register alto, with daily vocal training.
- PJ is a recently retired scientist, who used in his youth to study and play viola. He remains an attentive music listener.
- GJ is a lady, music lover, participating in amateur choir performance.
- FXS teaches piano in a music school, and contributes to choral courses.
All subjects other than PB are free of hearing problems or defects, and are considered as normal listeners.
2.4. Procedures
An ordinary interval trial consists, after listening to a reference tone during a short while and ceasing emission, to adjust a second tone to the prescribed interval. To obtain a minimum statistic basis, several trials of the same interval at the same reference pitch are necessary, but in order to prevent biasing of results by unintentional memorizing, the memory of each trial has to be erased before operating again at same conditions. An empirical erasing rule requires that at least three trials at very different frequencies be made between trials at same conditions. So any interval experiment must include at least 4 starting frequencies in a session.
Interval adjustment experiments require acute attention, and are nervously straining. So experimental sessions cannot extend reasonably beyond about one hour, which limits the total number of trials, and then the statistical richness of results. Certain subjects are somewhat puzzled by the operation of the STGPR, and cannot achieve much more than 50 trials per session, which gives, with 4 starting frequencies, a little more than 12 trials per frequency. Subject PB who is fully accustomed to the STGPR control may achieve sessions of 60 to 100 trials, but often his sessions are limited to half an hour with 15 trials per frequency, on account of brain straining.
Musical specialists often state that the average music listener is accustomed to the standard tempered musical scale, and has this scale unconsciously present at brain. Though improbable, this possibility has been taken into account in the present work by always choosing starting frequencies at mid distance of tempered notes i.e. a quarter tone apart the usual degrees (based on medium A at 440 Hz). A such "shifted scale" has been established and described in terms of numbered "positions". Position 1 is arbitrarily fixed at 63.544 Hz, Position 2 is 100 cents above (67.323 Hz), and so on in increasing order by semitone steps, up to Position 62, at 2154.334 Hz, a practical upper experimental limit.
For each session a rigid protocol is observed to respect the erasing condition. The trials at a same position are made on the melodic keys of a given round. Key MK0 is always tuned in advance to the reference position pitch, and keys MK1, MK2, etc, are the trial keys. Successive rounds are assigned to the different positions, in the order imposed by the protocol. At first, round n0 is activated, corresponding to position Pa. The reference tone of Pa is heard by touching (left hand) MK0, then the subject captures by right hand control CRWT the reference divider, and, releasing MK0, he or she presses with a left finger the trial key, e.g. MK1, which emits the same tone at reference pitch. Maintaining touch on MK1, and using the tuning controls the subject adjust the trial tone to the desired interval. This operation is left to the entire initiative of subject, who decides the duration of touching, and repeats as judged necessary the listening of reference and tuning refinements. Only the subject is not allowed during session to compare trial keys. Of course the display of divider is masked, except occasionally to check reference. Once a trial key has been adjusted, the round is switched to the following n1, corresponding to position Pb with a reference frequency very different from the preceding one, and a new adjustment is performed with MK1. Etc. If the session deals with 4 positions, after round n3 the n0 position is switched again, and a new adjustment is performed on a new trial key, e.g. MK2, and the cycle continues, changing round after each achievement. The individual trial achievements are hand checked by pencil ticks on a double entry table.
The control keyboard assigned to right hand includes 4 keys. The bottom palm key touching induces an access to the memory corresponding to the chosen round number and pressed melodic key, and submits the divider stored in this memory to the adjusting action of the three right middle fingers keys. The middle key has a progressive action. A slight initial touching switches in the "write" command, then a normal pressing enables the up-down counter, the output of which is the binary divider number d, displayed on board in octal system. The index finger key, when pressed, switches the counter to up counting, lowering the tone pitch. When this key is free, with the middle key active, the counting goes down and the tone frequency increases. The right finger key, when pressed, simply accelerates the counting by a factor of 4, necessary in low pitch range to shorten the tuning process.
The operation of these adjustment controls differs from usual tuning means, such as potentiometer knobs. It does not offer the possibility of memorizing given frequency changes, since the frequency variation is a function of three parameters, the strength of pressing, the duration of touch, and the frequency itself. Very short and slight touching permits sufficiently small changes, ensuing tuning precision.
After achievement of all the adjustments of a session, or eventually several, the divider numbers stored in M are read by playing again the rounds and melodic keys assigned to the session(s), and inscribed in a table file of a personal computer, for registering and processing (computing pitches or intervals), and finally editing in form of tables or graphics.
3. Two timbres unison experiments
3.1. Experiments and unison procedure
After fortuitous observation by author of significant subjective pitch change of a complex tone when the timbre was suddenly switched to a quite different harmonic composition, many experiments were done to measure this effect more precisely. Two typical examples of such experiments are exposed below.
Experiment Ia consisted, after hearing a colored reference tone, to switch silently the timbre to pure tone and adjust on a trial key this new stimulus to the subjective pitch of the former. Since the pure tone is composed of only a fundamental, the resulting tuned physical pitch is assumed to equal the subjective colored tone pitch, and the eventual difference in physical frequencies measures the timbre pitch shift effect.
The subject was the author PB-LE, in monaural left hearing. The colored tone was Sesquialtera. The procedure for unison is somewhat different from that described in preceding section, which concerns ordinary intervals. Here the trial keys are to be pre-mistuned, and the deviation chosen has been 350 cents, intermediary between minor and major thirds. Odd number trial keys were lowered, and even were raised. The explored positions were n° 9, 18, 27, 36, corresponding to respective frequencies of 100.9, 169.6, 285.3, 479.8 Hertz.
Since no particular musical interval was concerned, the protocol assigned the four positions to respective successive rounds n° 34-37. After hearing the reference timbre (Sesquialtera) on round 34 (position 9) and reference key KM0, the timbre is switched to Sinonde, and key KM1 (pre-lowered) is tuned on position 9, after which the timbre is switched back to reference (Sesquialtera). The round is changed to n°35 (position 18) and after hearing reference, KM1 is tuned on Sinonde, and the same process with KM1 is followed on rounds 36, 37. The sequence is then resumed with key KM2 (pre-raised) on rounds 34-37, and with the other keys KM3-KM13 and barred KM17-KM29, for a total of 104 elementary trials. Until the 104 trials are through, any direct comparison of trial keys or playing a trial key with the reference timbre are strictly prohibited.
In Experiment Ib the subject was again author but with aided right ear (PBa). The reference tone was flute F1, and the trial tone was Octave Choir. Positions explored were n° 12, 20, 24, 32, 36, 37, corresponding to respective frequencies of 120, 190.4, 239.9, 380.8, 479.8, 508.4 Hz. Ten trials were done per position for a total of 60 trials, after the same pre-mistunings as in Exp.Ia. The successive six rounds n° 20-25 were assigned respectively to positions 20, 37, 32, 24, 36, 12.
3.2. Results
The result of unison Experiment Ia is illustrated in Figure 3, which gives the four mean shifts, with standard deviation bars (see also data Table A in Appendix II). Separate analysis of trials mistuned in the same direction did not show any significant influence on results of the mistuning direction. A repeat of the experiment gave a quite similar result. Also the spreads did not exhibit a noticeable tendency to split into separate groups.
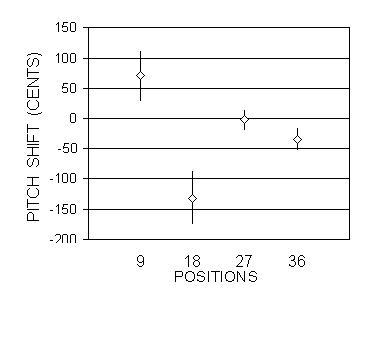 |
Figure 3. Subjective pitch shifts observed in changing timbre from Sesquialtera to Sinonde, by hearing-impaired subject PB-LE (left monaural). Bars indicate two standard deviations. |
The main observed features are at low positions 9 and 18 the large shifts (respectively of +71 and -132 cents), and the very large spreads (at position 18 the SD is 51 cents). At position 27 the shift is very small with a total spread of only 17 cents.
 |
Figure 4. Subjective pitch shifts by changing timbre from flute F1 to Octave Choir. Right monaural hearing by aided subject PBa. Bars indicate two standard deviations. |
Experiment Ib results are displayed in Figure 4, which features large positive shifts in the upper frequency region with reasonable spreads (SD of 8 to 16 cents) (see also data Table B in Appendix II).
The main observed features are the large shifts at upper frequencies, with at position 36 a shift exceeding 100 cents and a quite small spread.
4. Discussion I
4.1. Unison experiments consequences
In Experiment Ia the complex reference tone is essentially composed of a weak fundamental, strong n°3 and n°5 harmonics, a few weaker higher odd harmonics, and no even harmonic. As may be seen in Figure 3, at position 18 (169.64 Hz), a very conspicuous negative shift of more than a semitone is recorded, signifying that the subjective pitch of the colored reference tone deviates downwards from the fundamental level, which remains at the physical pitch (169.64 Hz).
In Experiment Ib, the reference tone is a flute where an overwhelming fundamental allows the confusing of physical and subjective pitches. The matching tone is Octave Choir, with a weak fundamental partial, and essentially strong harmonics n° 2 and 4. At position 36 (479.8 Hz) a positive shift of more than a semitone is observed with a relatively small spread, indicating that the subjective colored pitch deviates downwards from physical fundamental, like in the preceding example. Here the frequency is in a range where the hearing-impaired subject does not show abnormal spreads with pure tones, as could be the case in the former experiment.
Such important subjective pitch shifts can obviously be related to hearing defects in the subject, leading to two kinds of inescapable deductions :
First, the hearing defects imply some abnormal or irregular frequency distribution somewhere in the hearing system.
Second, the strong low order harmonics happen to be capable of forcing a pitch choice markedly deviating from the normal value (the physical value), which therefore suggests the existence of permanent links connecting harmonic levels to a frequency region around subjective fundamental level.
4.2. A tone hearing model
The last deduction leads directly to the concept of a "tone hearing model", applicable to a central pitch processor such as those considered in all modern psychoacoustical theories. Such a central pitch processor unit can be viewed as an assembly of numerous groups of neurons, each group selectively dedicated to a particular frequency of the auditory range. These groups are arranged spatially in continuous frequency order, with approximate logarithmic spacing. In each group, particular neurons, which could be called "central input neurons", receive the signals transmitted from both cochleae by the auditory nerve fibers and intermediate stages. In the present model, these input neurons develop along frequency axis downward axons which connect themselves to lower frequency levels the frequencies of which are in integer ratios with the original frequency, 1/2, 1/3, 1/4, etc.. When excited during the hearing of a complex tone, the concerned central input neurons instantly and automatically retransmit the signals downwards. Since the concerned lower levels constitute a subharmonic pattern, this hearing concept could be called a "subharmonic retransmission model". When the heard tone is a pure tone, there is only one set of lower excited levels, forming a subharmonic grid. If the tone is a complex one, then there will be as many separate subharmonic grids as there are active partials in the stimulus. The multiple subharmonic diffusion will give rise to neuronal convergences at the levels receiving several simultaneous excitations, and if the tone is harmonic, there will exist in particular a strong convergence at fundamental level. This scheme is quite similar to that of Terhardt (Ref.3), except that it is not supposed to comply with any theoretical formula or mathematical law, being just the result of a natural forming process (see below). It is consistent with a number of facts and experiments in auditory field. In particular, it explains very well the perception of missing fundamentals, and the existence of perfect chords in harmony. The existence of detectable subharmonic levels of pure tones has been shown by Houtgast (Ref.4). Pure tone subharmonics are also the only possible explanation of successful performance of simple melodic intervals such as octaves with pure tones (Ref.1,2). Beyond the strictly spatial features just described, temporal aspects may also be taken into account. If the input neurons re-transmit downwards input pulses at unchanged rhythm, then the lower spatial convergences will be accompanied by timing convergences. At fundamental level, the multiple pulses coming from harmonic levels will result in a periodic global excitation locally tuned, thus contributing to the final pitch perception.
4.3. Central processor development
The development of subharmonic axons and synapses could take place in utero, but also after birth, through environmental auditory experiences. Supposing for example at birth descending axons emitted by input neurons, the hearing of rich harmonic sounds could induce in the infant central processor synaptic contacts between these axons and local neurons at levels where occurred signal coincidence. For that the baby's own cries, at start, and a little later the infant's own vowels, would constitute perfectly suited stimuli, in addition to the various environmental events. After extensive auditory exposure, the central hearing system would be wired over the entire auditory frequency range . Of course, along youth, repeated experiences of rich tones, at convenient loudness, in particular hearing consonant music, would be a favourable factor to fashion a musically capable hearing system. Inversely total absence of musical background in youth would very probably result later in poor musical aptitudes. Since a great majority of environment tones are harmonic (vowels, cries..) the infant auditory system will develop axonal links of the accurate lengths corresponding to the integer ratios inherent in the frequencies of every periodic tone. Later the individual's cortex and cochleae will grow independently in size, which might alter somewhat the original perfection of the system. For example extreme experiences might be imposed to ears, damaging perhaps peripheral parts. Altering of deeper parts is less likely, but one may wonder about the necessary stretching of axons to cope with cortex development. Surely, continuous favourable auditory environment during early years and youth would be a decisive factor for maintaining accuracy and self-consistency of the different parts of the auditory system.
4.4. Location of frequency irregularities
Now, the question remains of the location of the frequency distribution irregularities observed in a hearing impaired individual. Two preferential sites may be thought of : at the basilar membrane (peripheral), or inside the pitch processor (central). To explain the observed spectral pitch shifts, displacements from normal place of frequency responses along the basilar membrane would suit. Assuming normality of upper auditory parts, the tonotopic organization of nerve fibers and frequency levels of central processor would transmit or receive wrong information, and then extract a mistuned pitch.
A central location of the frequency distribution irregularities would suppose practically wrong lengths of subharmonic connections. Considering the subject's hearing defects as having most probably be caused by abnormally loud noise shocks, the peripheral defect location appears much more likely than the central possibility. This hypothesis will thus be assumed in the remaining of the present paper, and in particular the central processor of impaired subject PB will be supposed normal. We do not know to which degree of accuracy subharmonic links lengths correspond to frequency integer ratios. There might exist small deviations, and anyway neurons occupy space, which imposes a limit to frequency discrimination. Moreover, one must not forget the small peripheral irregularities accounting for diplacusis in normal listeners. These small defects are reflected in the central pitch processor, where they appear undistinguishable from eventual intrinsic defects.
Although the present paper does not deal in anyway with the exact location of the central pitch processor inside brain, a location in cortex is understood as the more likely on account of recognized continuous tonotopic correspondence with cochlea of the main cortical auditory areas. Also Houtsma and Goldstein proved a central origin of complex tones pitches (Ref.5). However recent works suggest possibility of pitch extraction within the inferior colliculus, with a particular spatial organization (critical bandwidth laminae) (Ref.6).
4.5. Labeling levels
In any case some labeling appears necessary to designate and distinguish the different central frequency levels excited in hearing a periodic tone. In the proposed coding X[m/n], the brackets indicate a labeling and not a quantity, X designates the tone or auditory object, m is the order of an active harmonic of X, and n the order of a subharmonic issued from X[m], lying at designated level. For example, when hearing a periodic tone R, R[4/2] will designate the subharmonic level of second order descending from the fourth harmonic of R. In Experiment Ia the subjective pitch of the tone S is assumed to result essentially of the convergence of subharmonic levels S[5/5] and S[3/3], which at certain frequencies (e.g. positions 9 and 18) deviates from the fundamental S[1]. Similarly in Experiment Ib the subjective pitch of complex tone C is supposed to result essentially from focussing of levels C[4/4] and C[2/2], eventually separated from the physical fundamental C[1].
Assuming the subharmonic retransmission model, one can observe that in Experiment Ia the main primary cues are the largely spaced harmonics n°3 and 5, and that might exist other possible efficient convergences, for example S[5/10],S[3/6] at inferior octave, or S[5/15],S[3/9] at inferior twelfth, which could offer subjective pitch alternatives. In this experiment, the presence of a weak fundamental, although neglected for accurate pitch, appears to constitute an essential cue in pointing to the frequency bandwidth to be considered for pitch choice. In Experiment Ib, the small fundamental inhibits the obvious attractive convergence C[4/2],C[2], one octave higher.
Two additional comments must be made. First, the essentially spatial origin assumed for the deviated pitches of Experiments Ia and Ib signifies that the temporal factors are neglected, since the registered frequencies of stimuli are probably not altered by eventual basilar responses displacements, and thus timing convergences ought to occur at physical fundamental level. In short, spatial cues seem to override temporal cues.
Second, to issue a definite pitch a convergence does not need to be perfect. Most often the convergences will be only approximate, with some moderate scattering of the participating subharmonic levels. In normal binaural hearing the respective contributions of the two ears do not exactly coincide because of diplacusis, and yet the central unit succeeds in extracting a satisfactory unique pitch. In this respect some experiments of Shouten et al. (Ref.7) offer a particularly suited illustration. In those experiments some definite low pitches have been perceived in complex inharmonic stimuli composed of three pure tones. For example when the components are at 1700, 1900, 2100 Hz, listeners agree to a low sensed pitch around 188 Hz, quite different from the value of 200 Hz separating consecutive partials. Such a frequency lies close to a subharmonic approximate convergence of levels (1700)[1/9],(1900)[1/10],(2100)[1/11], giving a theoretical mean of 187.8 Hz with a total spread of 2 Hz. But the authors discovered that the listeners made sometimes stray matchings, the frequencies of which also fall near possible convergences. In the case cited above a second matching appears at about 215 Hz, concerning possibly a grouping of levels (1700)[1/8],(1900)[1/9],(2100)[1/10]. Even with a harmonic stimulus of fundamental pitch 200 Hz (missing), when the subjects are instructed to search for additional matchings, they succeed in obtaining such extra pitches. For example at a central frequency of 2000 Hz, beside the straightforward 200 Hz, they found secondary matchings at about 222, 178, 162 Hz, near possible respective convergences (1800)[1/8],(2000)[1/9],(2200)[1/10] /(1800)[1/10],(2000)[1/11],(2200)[1/12] /(1800)[1/11],(2000) [1/12],(2200)[1/13].
4.6. Cognitive operation
So within the pitch processing a decisive stage of cognitive operation appears to take place, that can be described as an integrated voluntary intervention, taking into account all available cues, temporal as well as spatial, and different in nature of the direct responses of neurons and neuronal arrays which can be understood as automatic, mechanical, passive. This cognitive aspect is obviously present in the Shouten experiments above mentioned, where guided attention of listeners may bias the result. In Houtgast experiments (Ref.4), pure tone subharmonics can be detected only when the subject's attention is drawn to the proper frequency zone.
5. Interval experiments
The following interval experiments concern only descending intervals, because preliminary trials seemed to indicate lesser spreads than in ascending. Later work have shown irrelevance of interval direction with respect to melodic interval values, in accordance with the general feeling of acoustics scientists.
5.1. Octaves A
Descending octave monaural (right ear) adjustments have been made by four listeners over a same set of starting frequencies, with timbres of Octave Choir and Sesquialtera. The listeners were normal hearing CR, PJ, GJ, and hearing impaired PBa wearing an auditory aid. In addition CR and PBa performed same octaves with Sinonde, and PBa also tried Trompe and Cromorn. Starting positions were 21, 29, 37, 45 (i.e. frequencies 201.7, 320.2, 508.4, 807 Hz). The protocol order of tried positions was 21, 37, 45, 29, avoiding the double octave succession 45, 21. The number of trials varied somewhat depending of listener or timbre. PG and GJ made in all 52 trials each per timbre. CR made 56. PBa made 100 trials per timbre except Sinonde with only 60.
Results appear on Figure 5 which gives mean octave values with standard deviation bars, for each listener (see also data Table C in Appendix II). The lines joining points only contribute to timbre discrimination.
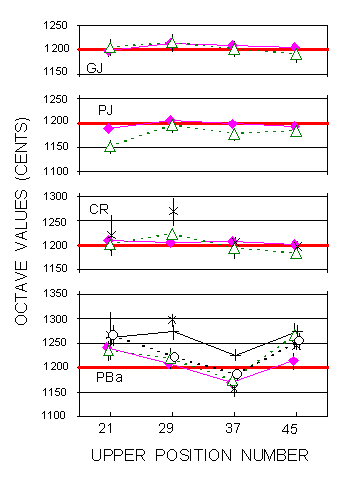 |
Figure 5. Values of descending octaves adjusted by 4 listeners from 4 positions. Right ear monaural listening, PBa using an hearing aid. Symbols for timbres : Sinonde : slanted crosses, no line (only CR, PBa). Octave Choir : filled diamonds, solid line. Sesquialtera : unfilled triangles, dashed line. Trompe : upright crosses, solid line. Cromorn : unfilled circles, dashed line. Some symbols are slightly shifted aside to improve legibility. |
The main general observation is the clear superiority of Octave Choir over else timbres, in terms of justness as well as precision, although Sesquialtera keeps rather close in these respects. The Sinonde results show rather large deviations and spreads at the two low positions, for both concerned listeners. The two rich timbres of Trompe and Cromorn by PBa give rather precise responses, and Trompe exhibits a clear tendency to enlarge octaves, by around a quarter tone. For the other timbres, the so-called octave enlargement is not clearly observed, and even is contradicted by PJ with Sesquialtera. The following table gives more details about Octave Choir to supplement Figure 5.
| Table I |
| Mean values and (SD) in cents of descending octaves in timbre Octave Choir |
| Subjects | Position 21 | Position 37 | Position 45 | Position 29 |
| GJ | 1197(11) | 1212(10) | 1208(10) | 1205(9) |
| PJ | 1189(11) | 1204(6) | 1198(3) | 1192(4) |
| CR | 1209(7) | 1205(5) | 1208(4) | 1201(3) |
| PBa | 1242(10) | 1209(8) | 1169(10) | 1214(18) |
A few unintentional abnormal interval tunings are worth mentioning. PJ missed once the octave in Octave Choir from position 37 and tuned to a double octave. GJ did twice a double octave with Octave Choir from position 45, another double octave with Sesquialtera from position 45, and a fifth from position 29. Table II displays these stray adjustments.
| Table II |
| Unintentional tunings instead of octaves |
| Subjects | Timbre | Upper Position | Adjusted val.(ct) | Nearest Perfect |
| PJ | Octave Choir | 37 (508.4 Hz) | 2411 | 2400(15th) |
| GJ | Octave Choir | 45 (807.0 Hz) | 2410,2407 | 2400(15th) |
| GJ | Sesquialtera | 45 | 2432 | 2400(15th) |
| GJ | Sesquialtera | 29 (320.2 Hz) | 690 | 702 (5th) |
5.2. Octaves B
Normal hearing subject FXS made also octaves, in monaural hearing (left ear), in experimental conditions different from above. He made only 3 trials per case, descending from 9 positions ,i.e. 23,25,27,29,31,33,35,37,39,(frequencies 226.4, 254.2, 285.3, 320.2, 359.5, 403.5, 452.9, 508.4, 570.7 Hz), with Octave Choir, Sesquialtera and Sinonde, in all 81 octave trials. The protocol order of tried positions was 23,31,39,25,33,27,35,29,37. FXS's octaves are detailed in Figure 6. Although superiority of Octave Choir for octaves again appears, the two other timbres are not so less accurate, except Sinonde at positions 25 and 27 (see also data Table D in Appendix II).
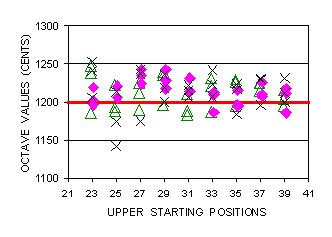 |
Figure 6. Descending octaves by FXS from 9 positions (226.4 to 570.7). Timbre coding : Filled diamonds for Octave Choir. Unfilled triangles for Sesquialtera. Crosses for Sinonde. For more display clarity symbols for Octave Choir and Sesquialtera have been slightly shifted to right and left. |
5.3. Octaves further analysis
In an effort to characterize more precisely the obvious influence of timbre over octaves quality, the data was reprocessed to focus on the tuning precision. For each subject and timbre the mean octave values of each position were subtracted from the trial values of this same position. The "deviations to means" thus obtained were gathered in (Subject,Timbre) groups, and the standard deviation of each group was computed as an "overall specific spread", the term "specific" meaning "for a particular subject, a particular interval, a particular timbre, and in a lesser measure a particular set of frequencies". This method was implemented with available octave data, and issued the values in cents displayed in Figure 7, where FXS's results were included despite very particular experimental conditions. Some previous results of PB (unaided right ear) not given in Figure 5 and Table I, with same conditions as Octaves A, are also mentioned in Figure 7.
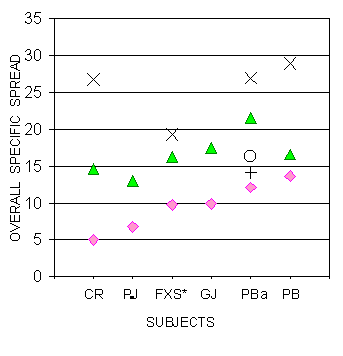 |
Figure 7. Overall specific spreads of octaves of different listeners. Timbre coding : Filled diamonds for Octave Choir. Triangles for Sesquialtera. Slanted crosses for Sinonde. Unfilled circle for Cromorn. Upright cross for Trompe. Subjects CR, PJ, GJ, operated in monaural right ear. FXS operated in monaural left ear. PBa operated in monaural aided right ear, and PB in monaural bare right ear. |
This presentation reveals several facts. First, the inequality of spread between subjects, with a clear superiority of CR, owing probably to continuous vocal musical training. Second, the different aptitudes of timbres to perform octaves, the Octave Choir mixture coming clearly ahead, followed by Sesquialtera and finally Sinonde very far except for subject FXS. For the only subject PBa the two rich timbres Trompe and Cromorn fall just after Octave Choir.
Another way to examine timbre influence on octave tuning precision consists in displaying the deviations to means of each group (Subject,Timbre) in increasing value order, with constant abscissa incrementing. This presentation refers more directly to experimental results, showing details which disappear in general averaging. Figure 8 gives such a presentation for data of Octaves A.
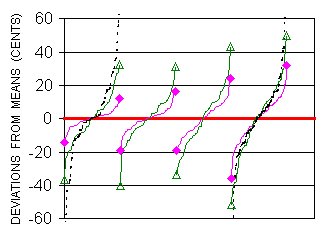 |
Figure 8. Distributions of deviations to means of octaves for 4 listeners and 3 timbres. The listeners are from left to right: CR, PJ, GJ, PBa. Presentation in increasing value order, with constant abscissae increments adjusted for equal widths among listeners and timbres. Symbols: Dashed line: Sinonde. Solid line and ending filled diamonds: Octave Choir. Solid line and ending unfilled triangles: Sesquialtera. A few points of Sinonde falling outside the ordinate limits have the following values : For CR +63.9, -62.6, -86.3. For PBa +93.4, -64, -66.8, -75. |
The curves for Octave Choir of Cr, PJ, and PBa are typical examples of gaussian or nearly gaussian distributions. Clearly the Sesquialtera points spread more than those of Octave Choir, and Sinonde exhibits very large deviations up to near a semitone for both concerned listeners, in accordance with data of Figure 7. Some stepwise discontinuities of curves are worth mentioning. In particular the Sesquialtera of PJ and GJ show several accidents of this type. Such stepwise features are still more marked for some separate frequency distributions of certain listeners (not shown). They occur mainly with Sesquialtera, but also with Octave Choir, and might correspond to spontaneous preferences in matching process.
All these results will be discussed more deeply farther in this paper, in the frame of the subharmonic retransmission model. As in this model interval tunings are supposed to result of central matchings between frequency levels, some intervals different from octave may appear useful to investigate. For example the interval of sixth may result of the matching of levels involving integers 3 and 5, since the perfect sixth is supposed to correspond to a frequency ratio of 5/3. For this the timbre Sesquialtera seems a priori particularly suited. As theoretical octave imply a frequency integer ratio, one may think of intervals implying other integers, for example 3 (interval of twelfth), 4 (fifteenth or double octave), 5 (seventeenth). Thus experiments implementing these different intervals have been effected.
5.4. Sixths
A few descending sixths have been made by subject FXS, in timbre Sesquialtera, from 7 starting positions (27,29,31,33,35,37,39), in 3 trials each. Figure 9 shows the corresponding 21 sixth values, which do not exhibit a significant tendency to cluster near the values 884 (theoretical perfect sixth) or 900 (tempered) (see also data Table E in Appendix II).
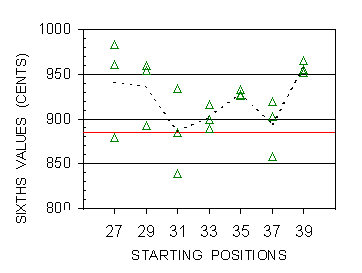 |
Figure 9. Descending sixths by subject FXS in Sesquialtera. Triangles correspond to the 21 individual adjustments from the different positions. Respective frequencies: 285.3, 320.2, 359.5, 403.5, 452.9, 508.4, 570.6 Hz. Horizontal line indicates the perfect value of 884 cents. Dashed line connects the means of positions values. |
A more thorough examination of sixths was made by PBa, in the two colored timbres of Octave Choir and Sesquialtera. There were 11 starting positions from 18 to 48, in the protocol order 18,24,30,36,42,48,21,27,33,39,45, and six trials per position per timbre, resulting in a total of 66 trials per timbre session. This test is illustrated in Figure 10 (see also data Table F in Appendix II).
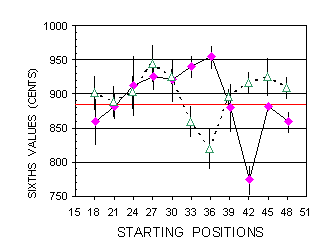 |
Figure 10. Descending sixths of subject PBa from 11 positions ranging from 169.6 to 959.6 Hz by 300 cents steps (respective frequencies: 169.6, 201.7, 239.9, 285.3, 320.2, 339.3, 359.5, 403.5, 452.9, 479.8, 508.4, 570.6, 678.6, 807.0, 959.6 Hz). Symbols : Octave Choir, filled diamonds and solid line. Sesquialtera, unfilled triangles and dashed line. The red horizontal line marks the 884 cents theoretical sixth value (frequency ratio 5/3). Slight aside shifts for more legibility. |
Considerable discrepancies between the timbre responses appear at certain positions, indicating different matching processes. But data analysis for matching precision shows only a slight superiority of Sesquialtera over Octave Choir, the distribution curves merging practically (see Appendix III, Figure 10apx).
5.5. Twelfths, Fifteenths, Seventeenths
After her octave sessions Subject CR was asked to try twelfth, a somewhat unfamiliar melodic occurrence. She made on Sesquialtera 14 trials per position from positions 28,34,39,45, i.e. frequencies 302.3, 427.5, 570.6, 807 Hz, in all 56 trials (protocol order 28,39,45,34). Her adjustments seemed straightforward, and the results were rather accurate, except more spread at position 34, as may be seen on Figure 11 (see (see also data Table G in Appendix II). Besides, her twelfths exhibit a clear tendency to exceed the theoretical frequency ratio 3, by about 20 cents. PBa made also descending twelfths from the same positions with Octave Choir, Sesquialtera, and Sinonde, 60 trials each. Figure 11 gives the mean values and SD bars of PBa and CR twelfths.
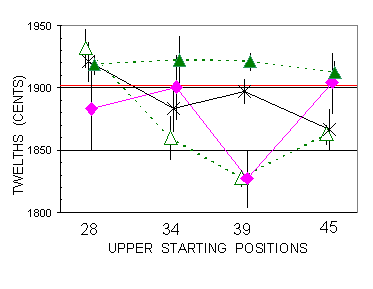 |
Figure 11. Descending twelfths by subjects PBa and CR, from 4 positions. Symbols : filled triangles and dashed line for Subject CR and Sesquialtera. Unfilled triangles and dashed line for PBa and Sesquialtera. Crosses and thin line for PBa and Sinonde. Filled diamonds and solid line for PBa and Octave Choir. The thick horizontal line at 1902 cents corresponds to theoretical twelfth (frequency ratio 3). Slight aside shifts for more legibility. |
To perform his twelfths PB was obliged to operate by mental cascading, i.e. to imagine an intermediary level, either a low octave followed by a low fifth, or the same in inverted order, fifth then octave. After hearing the reference tone the subject descends mentally one octave (or fifth), then a fifth (or octave), to situate the zone where the target is expected. Once this zone is acquired, the mental intermediary is dismissed, and the adjustment finalized directly, in comparing reference to real interval tone.
Figure 11 reveals strange features concerning PBa results. A clear superiority of Sesquialtera was expected (as in CR results), but the justness of Sinonde appears somewhat better, and Octave Choir is at least as good. To further analyze precision, the twelfth data has been reprocessed to compute the deviations from means of descending twelfths of CR and PBa, which appear in Figure 12. One curve stands out clearly in Figure 12, the Octave Choir curve, likely indicating a specific matching problem for this timbre and the interval of twelfth. The three other curves are rather close and similar.
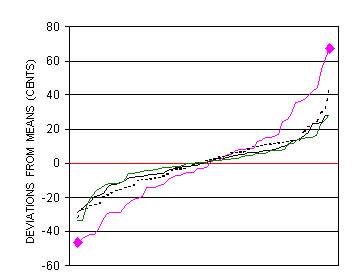 |
Figure 12. Distributions of deviations from means of descending twelfths of subjects CR and PBa. Presentation in increasing order, with adjusted abscissae for equal horizontal widths of curves. Symbols : Thin solid line for CR and Sesquialtera. Thin solid line ended by filled diamonds for PBa and Octave Choir. Thick solid line for PBa and Sesquialtera. Thick dashed line for PBa and Sinonde. |
To extend the explored domain of integer intervals, PB tried some descending double octaves, or fifteenths, and seventeenths.
The fifteenths were made from positions 33,38,43,48 (protocol order 33,43,38,48),in Octave Choir and Sesquialtera, with 15 trials per position per timbre. For these intervals, mental cascading was again necessary through an intermediary octave to locate the fifteenth pitch zone. The results appear in Figure 13, with comparable justness and precision among the timbres (see also data Table H in Appendix II). Trial points corresponding to unintentional fifteenths by PJ and GJ instead of octaves, at positions 37 and 45, have been added. A tendency to enlarge the double octave appears with Sesquialtera.
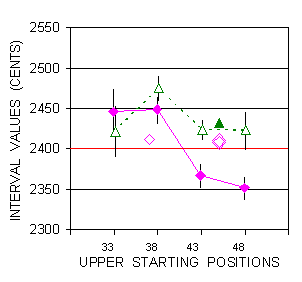 |
Figure 13. Descending fifteenths by subject PBa from positions 33,38,43,48 (frequencies 403.5, 538.6, 718.9, 959.6 Hz). Symbols : filled diamonds and solid line for Octave Choir. Unfilled triangles and dashed line for Sesquialtera. Thick horizontal line at 2400 marks theoretical perfect interval. Isolated unfilled diamonds and filled triangle refer to 4 unintentional fifteenths by subjects PJ and GJ at positions 37 and 45, during octave sessions (see Table II). Slight aside shifts for more legibility. |
The seventeenths were made also in Octave Choir and Sesquialtera from positions 36,40,44,48, i.e. frequencies 479.8, 604.5, 761.7, 959.6 Hz. Protocol order was 36,44,40,48, with 15 trials per position per timbre. Mental cascading implying two octaves and a major third permitted to locate the proper target bandwidth, before direct adjustment. Results are given in Figure 14, showing up to one semitone error at position 36 with Sesquialtera, and an enlargement tendency with Octave Choir (see also data Table H in Appendix II).
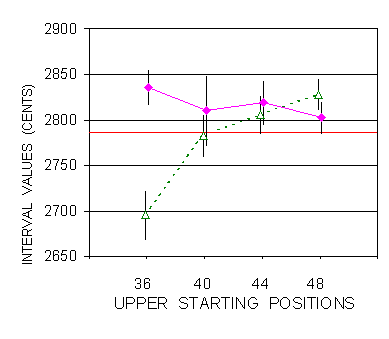 |
Figure 14. Descending seventeenths by subject PBa. Same symbols as in Figure 13 for PB. The thick line at 2786 indicates the perfect seventeenth (frequency ratio of 5). Slight aside shifts for more legibility. |
6. Discussion II
6.1. A preliminary question
The tone hearing model proposed in the preceding discussion section, in order to be confronted with interval experiments, must be included in a wider interval model, which will be considered hereafter. But before that, a preliminary question is to be examined, concerning the pertinence of the present research orientation, where a mental matching process is being supposed to offer the only way of melodic interval performance. Is this assumption totally founded, and do not exist other means of making accurate musical intervals?
Two main processes different from mental matching may be thought of. First, unconscious memorizing of standard musical pitches could result of frequent listening of tonal music scores, classic as well as jazz, folk, etc. This possibility cannot account for present interval results, where starting pitches differ systematically from standards by 50 cents (a quartertone). If standard pitches were engraved in listeners' mind, adjustments would have likely fixed on them, and the interval values been odd multiples of 50 cents. For example, trial octaves, instead of staying near 1200 cents, the theoretical perfect, would have rather fixed close to the standards at 1150 or 1250 cents, which was not observed. In fact, none of the tested intervals and listeners exhibited clear systematic tendency to fix on standards.
Second, gesture or muscular memory are known to permit rather accurate performances. Vocal artists and string players do indeed resort to this possibility. For example violin prestissimi require instinctive action excluding any fine adjustment. But in the present work, the sounds are produced by a machine and adjustments cannot be memorized because of the particular tuning process subject to three independent parameters (frequency, touching pressure, duration of touch). The large results spreads of PB, who is fully accustomed to this technique, compared to that of the external less accustomed subjects, is further evidence against muscular memory intervening in the present experiments.
A third unrealistic possibility must be mentioned. An asserted "tonal intoxication", owing nothing at all to physiological innate or natural deeds, would mean an acquired ability to make any theoretical interval from any starting frequency, which would imply long term memorizing of a multiple infinity of pitch couples, obviously beyond the capacity of human brain.
So a matching process will continue to be assumed as the way to make a melodic interval, apart from any short term memorizing of pertinent cue.
6.2. A melodic interval process model
In the preceding unison experiments, the matching addressed two proximate entities, supposed to be at same frequency, and no question was raised about what precisely matched what. Likewise, authors studying pure tone octaves do not seem to have asked themselves this kind of question. Ward (Ref.1), using octave judgments to establish a "scale of musical subjective pitches", only mentioned briefly mental "yardsticks" enabling perhaps musicians to produce codified intervals.
Ogushi (Ref.2), intending to explain the octave enlargement phenomenon and test his own pitch percept model, did not worry about the intimate nature of his octave adjustments. All other authors, when using such terms as "place theory", "spatial cues", etc, imply some sort of level matching, without going further into the process.
When considering various intervals and timbres, and contemplating possible tone harmonic content influence, one feels the necessity to detail further the successive steps implied in any melodic interval matching, and imagine a credible sequence of events.
Typically, for a complete and careful melodic interval adjustment:
- a reference tone R is listened to during a while
- at cessation of R, a fugacious memory of R, R', is left in mind for a short while
- a mental representation D' of a new tone at desired interval from R' is evoked and kept in mind
- a new real tone A is emitted and adjusted at the pitch of D'
- after this first tentative adjustment of A and ceasing A, R is heard again for checking, and appreciated versus the memory A' of A, while refreshing the memory R' of R
- a final adjustment matching A and R at desired interval through their images A' and R' is achieved by trial successive steps.
In this process entities appear such as R', D', A', which are not real tones but present an obvious attribute of pitch, plus eventually a character like a timbre. This sort of entities are generally called "auditory images", in analogy with optical domain.
Reviewing the successive steps of the process, one can distinguish a unison matching (D',A or A'), and interval matchings (R',D'), (A',R),or(R',A),or(R',A'). The first interval matching (R',D') is particular in that the pitch of D' is to be evoked directly at a definite interval from R' and thus can lack precision, just pointing to a pertinent pitch bandwidth. The other matchings are refinements of the former, tending to be as accurate as possible, and are the final real interval matchings.
One may also distinguish two kinds of auditory images. R', A', are mental replica of real tones just heard, and can present, in addition to pitch, features recalling the timbre of their real models. D' has also a pitch, but its color features are more doubtful, although D' may have inherited somewhat from R' in that respect. D' appears quite similar to the notes that musicians often sing to themselves in thought, in which the character of timbre is secondary. In addition, it seems highly probable that both types of auditory images are correlated only to mental spatial cues, without any oscillatory phenomenon or periodic neuronal firing.
On account of their key-role in melodic intervals, auditory images appear worth being granted a specific designation. The neologism "fantone" is proposed, a contraction of "fancied tone". Newly evoked fantones such as D' may be called "free fantones", while others like R',A', issued from heard real tones, may be called "replica fantones".
The experimental data concerning fantones is naturally scarce. Crowder (Ref.8) showed that listeners were able to include some timbre quality in evoked auditory images. Further, Pitt and Crowder (Ref.9) obtained evidence of mental imagery of timbre, and that this imagery was based primarily on spectral properties (and not on other cues such as tone attack). In the present paper, fantones will be examined mainly for their spectral properties, in light of interval results.
6.3. Examining interval results
Referring to results displayed in Tables I,II, and Figures 5-14, a first general remark is evidence of a matching process. In Figure 5, clear separation of different timbres responses at certain frequencies and for certain subjects, is evidence of an internal process correlated to spectral features, implying level matching. Individual interval variations with timbre are the result of idiosyncratic minor differences in basilar frequency responses. These details are enhanced by monaural listening, and would be practically erased by averaging results over several listeners. Inversely they appear widely accentuated in case of impaired listening, e.g. in PBa sixths, fifteenths, and seventeenths, displayed in Figures 10,13,14.
The remarkable precision of CR (octaves overall spread of 5 cents, less than 0.3 percent), with a favorable timbre, well separated from notes of standard musical scale, excludes any interval memory source. The large intervals of twelfths and more, practically never used in current melody, and the unintentional fifteenths of PJ and GJ (Table II, Figure 13), manifest the existence in brain of some permanent structures, materializing integer frequency relations.
For a deeper insight into interval results in order to improve fantones knowledge, it seems prudent to consider in a first round only the normal hearing subjects performances. Indeed PB probable frequency response irregularities might introduce misleading distortions in the structures to be investigated. Thus the main body of data taken into account will be the octave trials by FXS,CR,PJ,GJ, in the timbres of Octave Choir, Sesquialtera, and Sinonde. A glance at Figures 5-8 shows a glaring superiority of Octave Choir over the other tones to do octaves, which might be attributed simply to its octave relations between partials. In particular, if one of these partials played a direct role in the final matching, it would likely entail a frequency ratio at exact integer 2, or very near. But in contrast, Sesquialtera, which is totally deprived of this advantage, would logically give poorly accurate octaves. In fact the differences observed between the two timbres with respect to precision, are far from dramatic. On Figure 7 the Sesquialtera precision of PJ is better than the Octave Choir PB, and not much different from the O.C. of FXS and GJ (about 13 cents spread compared to 10). So a direct role of real partials in matching is very questionable. For octave (e.g. A descending from R), such a matching could be imagined between the levels A[2] and R'[1], or R[1] and A'[2], by hearing the real tone over the fantone and aligning the pertinent levels. From the modest difference in octave precision between the two timbres, it may be concluded that participation of real partials in octave matchings is either non-existent or very weak. In case of absence of partial participation, and assuming also no harmonic cue in fantones, the octave matching will occur between levels at or beneath fundamental. For instance, in Octave Choir, the presumed useful matchings could be enumerated as follows:
- A'([1],[2/2],[4/4]) with R'([1/2],[2/4],[4/8])
- A'([1/2],[2/4],[4/8]) with R'([1/4],[2/8])
- A'([1/3],[2/6],[4/12]) with R'([1/6],[2/12])
- A'([1/4],[2/8]) with R'[1/8]
- A'([1/5],[2/10]) with R'[1/10]
- A'([1/6],[2/12]) with R'[1/12]
- A'([1/7],[2/14]) with R'([1/14])
- A'([1/8],[2/16]) with R'([1/16])
In that presentation using the level coding proposed in Discussion I, the parentheses refer to neural convergences, A', R' are fantones respectively of adjusted and reference tones. Harmonic levels taken into account are limited to fundamentals and salient low order partials. Subharmonics of higher order than 16 are arbitrarily dropped to limit the size of display, assuming a probable decreasing effect with increasing order.
Similarly, octaves in Sesquialtera could be matched as follows:
- A'([1],[3/3],[5/5]) with R'([1/2],[3/6],[5/10])
- A'([1/2],[3/6],[5/10]) with R'([1/4],[3/12])
- A'([1/3],[3/9]) with R'[1/6]
- A'([1/4],[3/12]) with R'[1/8]
- A'([1/5],[3/15]) with R'([1/10])
The number of retransmitted cues involved with Sesquialtera (24) appears significantly less than with Octave Choir (31). This difference might be the true correlate of Sesquialtera inferiority for octaves, rather than a direct effect of partials oddness.
For Sinonde, the list of pertinent levels is more simple, involving only 16 useful cues: A'[1] with R'[1/2]
- A'[1/2] with R'[1/4]
- A'[1/3] with R'[1/6]
- A'[1/4] with R'[1/8]
- A'[1/5] with R'[1/10]
- A'[1/6] with R'[1/12]
- A'[1/7] with R'[1/14]
- A'[1/8] with R'[1/16]
The relative scarcity of pertinent cues might explain the poorer precision of pure tone octaves.
More specific assumptions are necessary to outline a likely fantone structure. First it can be supposed that free and pure tone fantones both comprise a fundamental level plus integer subharmonics at frequency ratios 1/2,1/3,1/4,... etc, with a probable decreasing influence with increasing order. Second, assuming the structure of replica fantones issued of colored tones to be similar to the former, inter-subharmonic levels, e.g. A[4/5], or A[3/5], falling between two successive integer subharmonics, are supposed not retained in fantone, for reason of simplicity. Thus replica fantones of colored tones would differ from free fantones only by having their levels reinforced by convergences issued from model tone harmonics.
In applying this structural model to a descending sixth interval, the matching in Octave Choir could concern the following levels:
- A'([1/5],[2/10]) with R'([1/3],[2/6],[4/12]).
And in Sesquialtera:
- A'([1/5],[3/15]) with R'([1/3],[3/9],[5/15]).
The same number of useful cues in both timbres (5 cues), is consistent with the very close spreads observed with subject PBa. However further research is needed to establish more firmly the fantone structures, and eventually modify the above proposed outline.
6.4. Present theory and other works
In view of the exceeding abundance of pertinent papers, the following comments will be restrained to a few prominent results presenting features which can be directly correlated to the present research, in addition to the previous remarks in Discussion I concerning Shouten's works.
6.4.1. Houtgast (Ref.4)
In his paper, Houtgast explicitly assumes subharmonic convergences to explain apparent harmonic oddness effects (second experiment).
6.4.2. Moore, Glasberg and Peters (Ref.10)
In these famous experiments the authors used multiharmonic stimuli (up to 12 components), and mistuned one of low order partials to observe the effect on the subjective pitch, measured monaurally by matching at unison with an adjustable comparison tone of very similar timbre. Their results, i.e. the shifts of subjective pitch versus mistuning, appear highly variable, with listener, mistuned order, and fundamental frequency. They conclude rightly to dominance of the first six partials in the perception of complex tone pitch.
The subharmonic retransmission model, combined with inevitable minor irregularities in the basilar membrane frequency responses (correlated to current diplacusis in normal listeners) may account for the observed queer disparity of results. The frequency response irregularities are reflected in central pitch processor as imperfect fundamental convergence of subharmonics issued of partials. When the retransmitted level of a given partial lies by chance near the convergence mean, its weight for shifting pitch is maximum, whereas if this level falls apart the mean its influence is lessened. As cochlear irregularities can be supposed more or less randomly distributed along the membrane, with individual idiosyncratic patterns, the apparent disorder of authors' data can be easily understood. The monaural listening implemented in this work has been of course a favorable factor to enhance peripheral irregularity effects.
6.4.3. Lin and Hartmann (Ref.11)
This work is part of a long series of researches aiming to improve knowledge of pitch perception. The paper deals with a "pitch shift gradient" concerning a mistuned harmonic embedded in a complex otherwise harmonic stimulus, varying several experimental parameters. When a harmonic is mistuned from its normal frequency, its subjective pitch, as measured by matching sequentially an adjustable pure tone, moves aside significantly from its physical frequency, in the same direction as mistuning, which seems to be exagerated. The pitch shift gradient cumulates the two opposite exagerations observed in each individual case, and is displayed in percent units as a pair of points with standard deviation bars. The vertical distance between the points constitutes the "gradient". On the figures it seems that abscissa is real physical frequency of mistuned harmonic, so the data for a given case appears as a tilted line segment joining two points. The mistunings are always of plus or minus 8%, quite a large move (greater than a semitone), insuring mistuned harmonic being clearly heard out of the basic complex stimulus, as a separate pure tone. The authors observed that "a large pitch shift occurs when the pair straddles a special frequency where a harmonic is supposed to be". For example in their first experiment, the mistuned harmonic was chosen within a gap of three consecutive orders (1-3 in case a), 2-4 in case b)) of a complex harmonic spectrum extending up to order 16. On the figures the pitch shifts are displayed by listener and plotted with respect to real mistuned frequencies, showing a conspicuous "zig-zag effect" illustrating the shift gradients, but also unexpected vertical shifts of the segments with respect to zero, positive or negative. In case Ib listener ST the six points are negative except one at zero, indicating negative displacements of the "cause" of the studied shifts from the theoretical harmonic situations (a displacement of about 1.4% appears in Ib/ST/mistuned order 1). These global vertical shifts are present more or less in all studied cases, but have not deserved quoting. The cause of exagerating shifts might be a masking effect created locally by subharmonic convergences occupying vacant harmonic places, issued from the upper real partials. For example, in case a) of first experiment, the vacant place 1 might be occupied by retransmissions ([4/4],[5/5],[6/6]----[16/16]), place 2 by ([4/2],[6/3],[8/4]---[16/8]), and place 3 by ([6/2],[9/3],[12/4],[15/5]). Similarly in case b) place 4 would be furnished by ([8/2],[12/3],[16/4]).
Two different aspects must be stressed. First, the minor cochlear defects will entail small displacements of real partials in the central pitch processor, with correlated convergence shifts despite minimizing influence of binaural listening. Second, the pitch shift gradient effect may depend of the strength of local convergence, itself function of the number of converging terms and eventually of convergence accuracy. So the gradient of case a) place 1, correlated to 13 converging terms, is much larger than that of case b) place 2 which is correlated to 7 terms. The gradients of case b) place 4 appear negligible, with only 3 pertinent terms. Results of third experiment in which the first partial is mistuned, in a variable harmonic neighboring, may be explained also by the diminishing strength of place 1 convergence when suppressing successively partial 2, 2 and 3, 2 to 4. But, in addition, the quasi-equality of gradients of cases b) and e) shows that there exist an important weighing of partial influence with partial order, since removing partial 2 alone has practically same effect as deleting partials 4-16 leaving only 2 and 3. The sixth experiment did not allow clear-cut deductions. In this experiment two cases were compared. In case a) a mistuned partial about 400 Hz was imbedded in a 200 Hz harmonic stimulus with partials 1 and 3 removed, and case b) used an 8 harmonics stimulus at 400 Hz with number 1 mistuned, in order to compare situations where local conditions around mistuned partial were identical. In a frame of subharmonic convergences case a) might be spoiled by spurious high order partials influence. At mistuned place 2 true convergences can only come from even higher partials, namely 4,6,8,10,12,14,16. But an interfering of odd partials is possible since the frequency differences of consecutive partials in region 13-16 are of same order as the mistuning (8%). For example partials 13 and 15 are bound to retransmit at levels [13/7],[15/7],[15/8], falling to 6 to 7 % from exact place 2, right in the mistuning range. In case b) the wider separation between high frequency partials reduces such interferences.
The authors conclude that the pitch shift results from a "contrast between the mistuned harmonic and a spectral pattern in the mind of the listener that serves as a template against which tones are compared". They are not specific about the formation of such a template and the present subharmonic retransmission model could supply useful hypotheses. It could also suggest new specific investigations, for example looking at what occurs at places 2 or 4 with a background harmonic tone comprising only odd partials, thus unable to raise efficient convergences.
6.4.4. Brunstrom and Roberts (Ref.12)
Like the preceding, this research aimed at gaining evidence of a harmonic template model of harmonic fusion. The authors used a hit-rate method to assess the perceptibility of a pure tone probe embedded in a harmonic background, with respect to probe position within a gap of 2-4 harmonic places (orders 6,7, or 6-8, or 6-9). The probe perception was effected through a sequential matching with an ajustable pure tone. Fundamental frequency of basic complex tone was randomly taken within a range of 200 Hz plus or minus 20%. There were 6 listeners and each displayed point resulted of 72 trials (first experiment) or 60 (second experiment). Essentially they found that hit-rates were high with probe between harmonic places, and dropped significantly, sometimes dramatically, at harmonic places. They concluded at existence of a template generated by the harmonic pattern even at places distant from real partials, the slots of which would inhibit an incoming probe.
In the works of Lin and Hartmann as well as Brunstrom and Roberts, a very important aspect seems to have been overlooked. Their experiments involve two successive separate situations, first hearing the proposed stimulus, second attempting a sequential matching. While hearing initial stimulus, the listener's perception encompasses two tones, a fixed harmonic complex, and a pure tone which can be mistuned from a harmonic place. After hearing, there remains only a memory of preceding sensation, and this memory may be quite different from the real stimulus, with perhaps a largely ill-known spectral structure. During the hearing phase, two clearly different situations are possible, and only two. A situation of fused perception, if the probe or mistuned element is acceptable as a harmonic member by its proximity to a harmonic place, or a situation of separate perception of two distinct tones. In the second case a matching is possible, not in the first. With a hit-rate method, the result is a mixture of successes and failures among several listeners, function of unknown basilar frequency responses, which renders difficult a definite conclusion. The apparent inhibition of real partials comes from the replacement after hearing of the real complex stimulus by one (or two) fantone(s), where harmonics are no longer present. However, a harmonic template could be asserted during hearing, if one supposed that vacant harmonic places are eventually occupied by convergences retransmitted from higher active partials. In Lin and Hartmann experiments the subjective pitch of mistuned partial is repelled from its physical value during hearing, and stands after hearing as the fantone pitch to be matched. In the matching phase no template action is likely.
6.5. Temporary conclusions
After experimental analysis and examination of related other works, the actual knowledge of melodic interval can be stated briefly as follows. A first periodic tone being heard, different places of basilar membrane are excited, and the excitations are fed to a central processor where corresponding input neurons receive the fragmented information. These input neurons retransmit the excitation to lower frequency levels in integer ratio with origins. When the stimulus ceases, input neurons come at rest and there remains a vanishing activity at excited low levels. This remnant constitutes an auditory image of previous real stimulus, called a fantone, with a specific structure of frequency levels keeping some memory of original real tone spectrum. The desired interval is realized first by mentally projecting another fantone, then a final matching is achieved by best aligning the proper levels of both fantones.
Many details of this description call for a review. For example the location of fantones is supposed to merge with the pitch processor, but could as well be in another central auditory area well connected with the processor. Modern imagery techniques (e.g. magnetic resonance) could probably clear up the question. Only "integer" levels of fantones have been considered here, and a definite pitch has been supposed for each fantone, instead of the convergence more or less spread at origin. A fine structure remains possible. The elimination of retransmitted levels non-integer fractions of fantone fundamental would suppose some sort of automatic inhibition. Thus, many questions remain, demanding important further research.
7. Summary and final remarks
A fortuitous observation of timbre influence on subjective pitch in an impaired listener has led to a subharmonic retransmission model for tone hearing, and further to a melodic interval process model, involving auditory images, called here "fantones". A credible natural process to create in early months of life the subharmonic links has been proposed, which owes nothing at start to music hearing. Interval experiments have been performed to further investigate the possible structure of mental phenomena associated with hearing and melodic intervals. New experiments should be designed to confirm and complete the outlined theory of melodic interval. Monaural listening and individual separate study are essential assets to reveal intimate structure details.
Finally a natural basis for classic musical intervals and related musical scales appears indubitable.
Acknowledgments
Author is greatly indebted to François-Xavier Sinniger, Catherine Ravenne, Geneviève Jamet, and Pierre Jamet, for their patient and fruitful collaboration to experiments. Thanks are also due to Yves Galifret, Laurent Demany, Christian Ravenne, and Lucy Kukstas, for helpful information and advice.
References
- W. D. Ward. Subjective musical pitch.J. Acoust. Soc. Am. 26 1954 369-380
- Kengo Ogushi. The origin of tonality and a possible explanation of the octave enlargement phenomenon. J. Acoust. Soc. Am. 73 1983 1694-1700
- E. Terhardt. Pitch, consonance, and harmony. J. Acoust. Soc. Am. 55 1874 1061-1069
- T. Houtgast. Subharmonic pitches of a pure tone at low S/N ratio. J. Acoust. Soc. Am. 60 1976 405-409
- A. J. M. Houtsma and J. L. Goldstein. The central origin of the pitch of complex tones : evidence from musical recognition. J. Acoust. Soc. Am. 51 1972 520-529
- M. Braun. Auditory midbrain laminar structure appears adapted to f0 extraction : further evidence and implications of the double critical bandwidth. Hearing Research 129 1999 71-83.
- J. F. Schouten, R. J. Ritsma, and B. Lopes Cardozo. Pitch of the residue. J. Acoust. Soc. Am. 34 1962 1418-1424
- R. G. Crowder. Imagery for Musical Timbre. Journal of Experimental Psychology: Human Perception and Performance 15 n°3 1989 472-478.
- M. A. Pitt and R. G. Crowder. The Role of Spectral and Dynamic Cues in Imagery for Musical Timbre. Journal of Experimental Psychology: Human Perception and Performance 18 n°3 1992 728-738.
- B. C. J. Moore, B. R. Glasberg, and R. W. Peters. Relative dominance of individual partials in determining the pitch of complex tones. J. Acoust. Soc. Am. 77 1985 1853-1860
- J-Y. Lin and W. M. Hartmann. The pitch of a mistuned harmonic : Evidence for a template model. J. Acoust. Soc. Am. 103 1998 2608-2617
- J. M. Brunstrom and B. Roberts. Profiling the perceptual suppression of partials in periodic complex tones : Further evidence for a harmonic template. J. Acoust. Soc. Am. 104 1998 3511-3519
- Pierre Billaud. A machine for melodic experiments. Web site file http://membres.tripod/p2lb/stgpr.htm




